The knapsack problem and logistics

The knapsack problem is a common issue nowadays. Beyond its mathematical implications, it significantly impacts inventory management and logistics and storage operations.

What is the knapsack problem?

The knapsack problem (aka the backpack problem) is a space optimization challenge. It seeks to find the best possible combination of items to fill a storage or transportation unit load without exceeding its weight limit. Its ultimate goal is to fit the most valuable goods in a hypothetical knapsack. Therefore, in addition to the weight of the items, it considers their economic valuation and dimensions. In logistics, the objective is to load the highest possible value within the available space.

Since its creation, the knapsack problem has been applied to many sectors. Nevertheless, it’s especially relevant in the world of e-commerce logistics, shipping, and storage. This is why technological intralogistics solutions developers use the knapsack problem to optimize their order fulfillment processes.

What type of problem is the knapsack problem?

The knapsack problem is one of the 21 problems that mathematicians classify as NP-complete. These were documented by theoretical computer scientist Richard Karp in his 1972 work Reducibility among combinatorial problems. However, it has been studied since the late 19th century, when George Ballard Matthews published On the partition of numbers.

No efficient algorithmic solution has yet been identified for solving NP-complete problems. As a result, in the case of the knapsack problem, the aim is to reach an approximate conclusion that offers the best outcome. Another example of this type would be the traveling salesman problem.

There are various ways to approach the knapsack problem. The first is exhaustive search, which involves testing all possible combinations. The downside is that these grow exponentially and might not be entirely practical. Another method is dynamic programming and approximation, which finds a value close to the optimum.

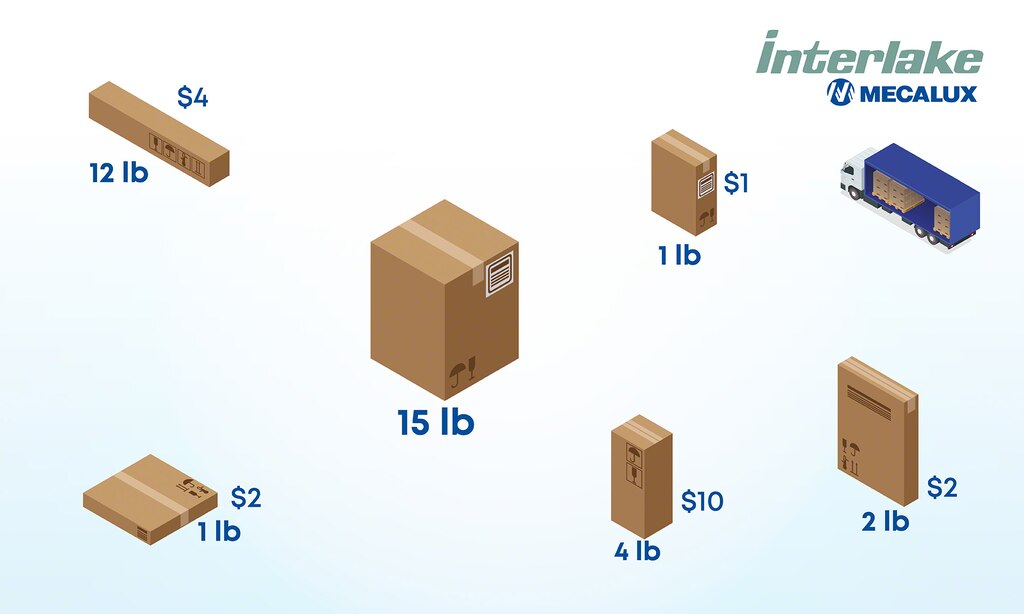
Applications of the knapsack problem

Though it may seem simple when viewed from a household perspective, the knapsack problem has various applications, particularly in logistics and supply chain management:

• Resource allocation. Just as the knapsack problem considers the value and weight of items to maximize the worth of the contents, it can also be applied to budget distribution. This approach allows for optimal results in real-life situations, such as organizing an event. The goal would be to increase visibility to the fullest by efficiently allocating the available budget across various activities to create a greater impact.
• Inventory management. Businesses have limited storage space, so optimizing it is crucial to multiply benefits and minimize costs. To leverage pallet, box, rack, shelf, and overall storage space, it’s advisable to use a warehouse management system like Easy WMS. This software can determine the order of shipments and how many items to include in each one.
• Cargo loading. Optimizing truck loading is similar to solving the knapsack problem. The goal is to maximize the value of the goods loaded without exceeding vehicle limitations. In this case, prioritization can be based on product pricing, delivery urgency, the route, and proximity to the destination. This principle also applies to passenger transportation in businesses such as airlines.
• Route planning. While more closely related to the traveling salesman problem, another application of the knapsack problem is in designing delivery routes. In this scenario, companies can determine which orders to ship on each trip based on their size, destination, and vehicle capacity.

How is the knapsack problem used in a warehouse?

In warehouse organization, the knapsack problem helps make the most of underutilized shelf space. It creates more locations for valuable items that can increase revenue. It also offers other advantages, such as placing the most in-demand pallets near pick stations for order processing and implementing the ABC analysis for classifying inventory.

Benefits of the knapsack problem

Applying the knapsack problem brings multiple organizational advantages:

• Greater utilization. As an optimization exercise, the knapsack problem enables the most efficient resource allocation, reducing the need for additional transportation and partially loaded pallets.
• Time and cost savings. Employing the knapsack problem minimizes resource waste and inventory shrinkage by encouraging efficient use of space and assets.
• Improved decision-making. It allows for evaluating different options through a data-driven system, analyzing multiple factors to select the most favorable choice.

Optimize your logistics processes with Interlake Mecalux

Looking to automate processes such as order fulfillment and enhance your company’s logistics operations? At Interlake Mecalux, we’re here to help. Our Easy WMS warehouse management system supervises both manual and automated facilities, ensuring real-time inventory control. Moreover, it can determine how many items to include in each shipment without exceeding weight restrictions. And if your company handles delicate goods alongside regular items, Easy WMS guides operators on which to pick first. Contact us for no-obligation advice on this and other storage systems we’ve been developing since 1966.